We describe two new algorithms for macromolecular simulations: a truncated Newton method for potential energy minimization and an implicit integration scheme for molecular dynamics (MD). The truncated Newton algorithm is specifically adapted for large-scale potential energy functions. It uses analytic second derivatives and exploits the separability structure of the Hessian into bonded and nonbonded terms. The method is rapidly convergent (with a quadratic convergence rate) and allows variations for avoiding analytic computation of the nonbonded Hessian terms. The MD algorithm combines the implicit Euler scheme for integration with the Langevin dynamics formulation. The implicit scheme permits a wide range of time steps without loss of numerical stability. In turn, it requires that a nonlinear system be solved at every step. We accomplish this task by formulating a related minimization problem-not to be confused with minimization of the potential energy-that can be solved rapidly with frequency (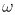_c) which in particular, can be used to mimic the quantum-mechanical discrimination among activity of the various vibrational modes.

Click to go back to the publication list

Webpage design by Igor Zilberman